Potęgowanie to podstawa matematyki, na której opiera się wiele znanych wzorów. Dlatego też chcąc dobrze zdać maturę z matematyki lub po prostu zgłębiając tę piękną dziedzinę jaką jest matematyka, należy dobrze zapoznać się z wzorami potęgowania oraz sposobami ich wykorzystania. Poniższy artykuł zapozna Cię z tym tematem.
Potęga to zapis mnożenia liczby przez siebie samą określoną liczbę razy. Dzięki temu, można uprościć zapis mnożenia, czyli przykładowo zamiast pisać 3 * 3 * 3 wystarczy zapisać 33. Można sobie łatwo wyobrazić jak bardzo jest to przydatne przy dłuższych zapisach mnożenia, gdzie tych liczb jest kilkanaście lub kilkadziesiąt.
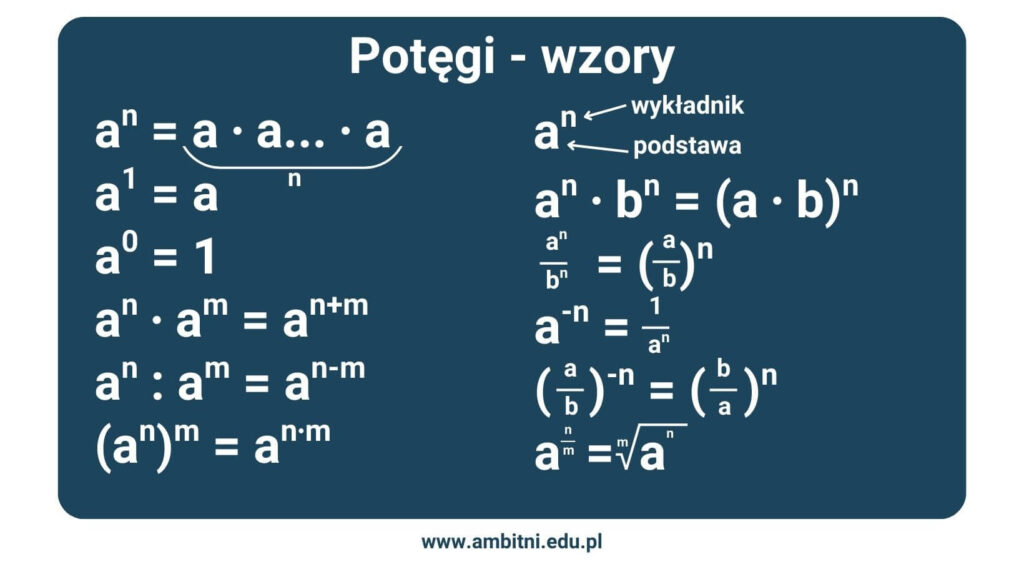
Zapis ogólny potęgowania: aⁿ = a * a * a …(n razy)... * a = x
gdzie:
Przykład:
23 = 2 × 2 × 2 = 8
Uwaga: Gdy wykładnik jest równy zero, wynikiem zawsze jest 1 (chyba, że w podstawie mamy 0, wtedy jest to symbol nieoznaczony).
Gdy podstawa jest ujemna dla parzystych wykładników, wynik jest dodatni, a dla nieparzystych ujemny. Przykład potęgi ujemnej:
-52 = (-5) * (-5) = 25, ale -53 = (-5) * (-5) * (-5) = -125
Co ciekawe, można stosunkowo łatwo usunąć minus z podstawy potęgi. Należy w tym celu odwrócić podstawę potęgi ujemnej. Przykładowo:
-an = (1/a)n
-52 = 1/52
-33 = 1/33
Podobnie gdy wykładnik jest ujemny można działać na odwrotności podstawy. Przykład:
a-n = (1/a)n
2-2 = (½)2 = ¼
Kwadrat danej liczby, to konkretna liczba podniesiona do drugiej potęgi. Czyli przykładowo:
a2
Czyli sześcian liczby 3, to: 32.
Sześcian danej liczby, to po prostu konkretna liczba podniesiona do trzeciej potęgi. Czyli przykładowo:
a3
Czyli sześcian liczby 3, to: 33.
Poniżej znajdziesz tabelę potęg od 1 do 10 w formie obrazka oraz tabeli. Wybierz odpowiednie przecięcie się kolumny i wiersza, żeby znaleźć interesujący Cię wynik.
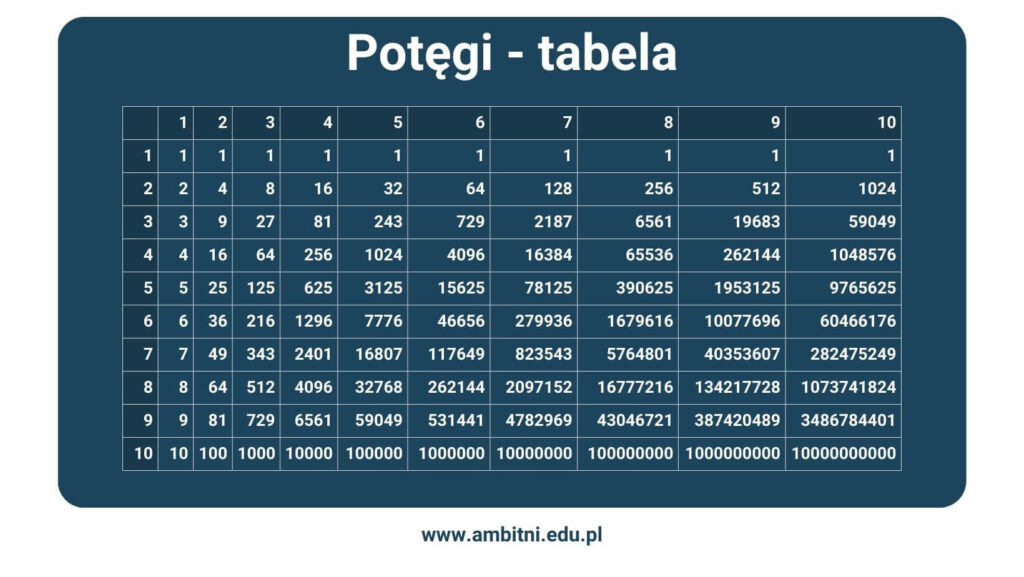
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Na potęgach można wykonywać rozmaite działania, takie jak dodawanie, odejmowanie, mnożenie, dzielenie, potęga potęgi, a także potęga iloczynu czy ilorazu. Poniżej znajdziesz odpowiednie wzory wymagane do poszczególnych działań oraz przykłady ich wykorzystania.
Nie ma gotowych wzorów dotyczących dodawania oraz odejmowania potęg o tych samych podstawach i wykładnikach. Jednak można uprościć zapis takiego działania, co przedstawiono poniżej.
Przykład:
315 + 315 = 2 x 315
3 x 315 + 315 = 4 x 315
315 - 315 = 0
2 x 315 + 315 = 3 x 315 = 316
3 x 315 - 315 = 2 x 315
Gdy mnożymy dwie potęgi o tej samej podstawie po prostu dodajemy wykładniki.
am × an = am+n
Przykład:
32 × 34 = 36 = 729
32 * (⅓)-2 = 32 * 32 = 34
Analogicznie w czasie dzielenia odejmujemy wykładniki
am ÷ an = am-n (dla a ≠ 0)
Przykład:
56 ÷ 52 = 54 = 625
Podnoszenie potęgi do potęgi polega na przemnożeniu wykładników.
(am)n = am*n
Przykład:
(23)2 = 26 = 64
Potęgowanie iloczynu polega na podniesieniu wszystkich elementów działania do danej potęgi.
(ab)n = an × bn
Przykład:
(2 × 5)3 = 103 = 1000 = 23 × 53 = 8 × 125 = 1000
Potęgowanie ilorazu działa w ten sam sposób co potęgowanie iloczynu.
(a/b)n = an / bn (dla b ≠ 0)
Przykład:
(3/4)2 = 32 / 42 = 9 / 16
Częstym błędem jest zapisywanie działań z potęgami w ten sposób:
22 + 32 = (2+3)2 = 52 = 25
Ten zapis jest niepoprawny i prawie nigdy nie uzyskamy poprawnego wyniku.
Poprawne rozwiązanie:
22 + 32 = 4 + 9 = 13
Gdy mamy do czynienia z tymi samymi składnikami działania:
32 + 32 = 2*32 = 2*9 = 18
Symbole nieoznaczone to wyrażenia matematyczne, których nie można jednoznacznie obliczyć, bo prowadzą do sprzecznych lub nieokreślonych wyników.
Przykłady:
Krótko mówiąc: symbol nieoznaczony to działanie, którego wynik nie jest określony w matematyce.
Kliknij w treść danego zadania z potęgowania, a pojawi się odpowiedź do niego. Z kolei pod linkiem zadania z potęgowania, możesz znaleźć więcej ćwiczeń z potęgowania. Zadania które się tam znajdują, mają rozwiązania krok po kroku, na końcu pliku.
Zadania z potęgowania - 50 zadań - kliknij aby pobrać
Potęgowanie to mnożenie tej samej liczby przez siebie wiele razy.
Ogólna postać: an = a · a · a …(n razy)... · a
Przykłady:23 = 2 · 2 · 2 = 8
54 = 5 · 5 · 5 · 5 = 625
102 = 10 · 10 = 100
am · an = a(m+n)
np. 23 · 24 = 2(3+4) = 27 = 128
Dzielenie potęg o tej samej podstawie:am / an = a(m-n), (a ≠ 0)
np. 56 / 52 = 5(6-2) = 54 = 625
Potęga potęgi:(am)n = a(m × n)
np. (32)4 = 3(2 × 4) = 38 = 6561
Potęga iloczynu:(a × b)n = an × bn
np. (2 × 5)3 = 23 · 53 = 8 · 125 = 1000
Potęga ułamka:(a/b)n = an / bn, (b ≠ 0)
np. (2/3)2 = 22 / 32 = 4/9
Najważniejsze wzory znajdziesz poniżej: